X^3 3x^2y 3xy^2y^3 (x y)^3 Solution Well you can use many methods to simplify like Using Pascal Triangle which give be 1, 3, 3, 1 as the expansion You can simplify (x y)^3 to either (x y) (x y) (x y) or (x y)^2 (x y) But using those two will result in sameSolutionShow Solution The given equation is (x y) 3 − (x − y) 3 − 6y (x 2 − y 2) = ky 2 Recall the formula `a^3 b^3 = (ab) (a^2 ab b^2)` Using the above formula, we have ` (xy)^3 (xy)^3 6y (x^2 y^2 )ky^2` `⇒ { (xy)^3 (xy)^3} 6y (x^2 y^2) = ky^2`Dy dx = c;

bestpictjg2x 最高のコレクション Simplify X Y 3 X Y 3 6y X Y X Y
(x y)^3-(x-y)^3-6y(x^2-y^2)=ky^2
(x y)^3-(x-y)^3-6y(x^2-y^2)=ky^2-The value of x for Algebra Linear Inequalities Help 8Up the triple integral I know that y 2 x 9 because y 9 is bounded and 9 y2 is not, and I also know 0 z xsince xis positive To get the y bounds, I have no additional information, and therefore I must set the x bounds equal y2 = 9 so 3 y 3The triple integral is 3 3 9 y2 x 0 18ydzdxdy= 3 3 9 y2 (18y)xdxdy= 3 3 (18y) 81 y4 2 dy



2
Simple and best practice solution for 3(x2)=y6 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,Are you sure you want to logout from your account?CANCEL Report an issue
Graph x^2y^24x6y3=0 Add to both sides of the equation Complete the square for Tap for more steps Use the form , to find the values of , , and to those of the standard form The variable represents the radius of the circle, represents the xoffset from the origin, and represents the yoffset from origin The center of the circle3 X Y x=y2 y=x2 (1,1) (4,2) Figure 2 The area between x = y2 and y = x − 2 split into two subregions If we slice the region between the two curves this way, we need to consider two different regions Where x > 1, the region's lower bound is the straight line For x < 1, however, the region's lower bound is the lower half of the2(5) 3y = 16 10 3y = 16 3y = 6 y = 2 So our solution is (5,2) or ELIMINATION METHOD xy =3 2x3y=16 I'm going to eliminate the y Multiply the top equation by 3 3(xy = 3) 2x3y = 16Simplify 3x3y=9 2x3y=16 Add the two equations together 5x 0y = 25 x = 5 Then substitute x=5 back into one of the original equations, let's use the
X • y • 2x "; The graphs of the lines 3x 4y = 2, 5x y = 11 and x ky = 2 all contain the same point asked in ALGEBRA 2 by chrisgirl Apprentice systemofequationsbygraphing x 2 2y 3 1 x y 3 3 Mathematics TopperLearningcom gl2kl500




Problem Sets 5 With Prof Edward Dowling Homework 5 Optimizing Functions Quadratic And Cubic Studocu




Oaszkzjza18qfm
Easy as pi (e) Unlock StepbyStep (x^2y^21)^3x^2y^3=0 Natural Language Math Input NEW Use textbook math notation to enter your math1 y = 2x 2 e x 3 /3 = x 2 y and y(0) = 2 by inspection 2 y = x 3 − 2 sin x, y(0) = 3 by inspection 3 (a) first order;Answer (1 of 5) The way it is given to you, it is almost obvious that it is (3xy)x² (3xy)2xy (3xy)y² = (3xy)(x²2xyy²) = (3xy)(xy)² However, if you don't notice that and just sum like terms together, you get 3x³ 5x²y xy² y³ = x³(t³ t² 5t 3), where t=y/x Now the roots of




Engineering Mathematics Notes



2
Solution for 2xy6xy3=0 equation Simplifying 2xy 6x y 3 = 0 Reorder the terms 3 6x 2xy y = 0 Solving 3 6x 2xy y = 0 Solving for variable 'x' Move all terms containing x to the left, all other terms to the right The inequalities are 2x 3y ≥ 6, x y ≥ 3 and y ≤ 2 Rewrite the inequalities so that solves for y , That's the slope intercept form and it will make the boundary line easier to graph 1) Draw the coordinate plane The first inequality 2x 3y ≥ 6 3y ≥ 2x 6 y ≥ ( 2/3)x 2 2) Graph the line y = ( 2/3)x 2 3) Since the inequality symbol is ≥ the boundary isExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music



Solve The Differential Equation Dy Dx X 2y 3 2x Y 3 Sarthaks Econnect Largest Online Education Community



2
(x;y) 2 R2 1 • x • 2;Systemofequationscalculator y= 4x3, y=x3 en Related Symbolab blog posts Middle School Math Solutions – Simultaneous Equations Calculator Solving simultaneous equations is one small algebra step further on from simple equations Symbolab math solutionsWe will use the elimination method to solve First, multiply (2) by 2 and add to (1) 7y = 2 ==> y= 2/7 Now substitute y= 2/7 in (2) x 2y= 3 x 2 (2/7) = 3 x 4/7= 3 Move 4/7 to the



1




Simplify X Y 3 X Y 3 6y X 2 Y 2
Facebook Whatsapp Transcript Ex 63, 11 Solve the following system of inequalities graphically 2x y ≥ 4, x y ≤ 3, 2x – 3y ≤ 6 First we solve 2x y ≥ 4 Lets first draw graph of 2x y = 4 Putting x = 0 in (1) 2 (0) y = 4 0 y = 4 y = 4 Putting y = 0 in (1) 2x (0) = 4 2x = 4 x = 4/2 x = 2 Points to be plotted are (0, 4), (2 If the linear equation in two variables 2x –y = 2, 3y –4x = 2and px–3y = 2are concurrent, then find the value of p If ܽa b = 35 and a − b = Two systems of equations are shown below System A 6x y = 2 −x − y = −3 System B 2x − 3y = −10 −x − y = −3 Which of the following statements is correct about the two systems of equations?



Apps Dtic Mil



2
Solution 1 First assume y 2 =ux 2, and y 2 '=2uxu'x 2 and y 2 ''=u''x 2 4u'x2u Substituting into x 2 y''2xy'6y=0 we get x 2 (u''x 2 4u'x2u)2x(2uxu'x 2)6y=0 and simplifying by adding like terms we get u''x 4 6u'x 3 =0 We reduce the order by w=u' to get w'x 4 6wx 3 =0 Now dividing by wx 4 and rearranging, we get and integrating both যদি (xy)^(3)(xy)^(3)6y(x^(2)y^(2))=ky^(2) , তারপরে কে = Updated On 23 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!(1 x) dy dx = (1 x)c = y (b) second order;




bestpictjg2x 最高のコレクション Simplify X Y 3 X Y 3 6y X Y X Y



Cbse 8 Math Cbse Factorization Ncert Solutions
Example If the lines 2x y – 3 = 0, 5x ky – 3 = 0 and 3x – y – 2 = 0 are concurrent, find the value of k Three lines are concurrent if they pass through a common point ie point of intersection of any two lines lies on the third line It is given that lines 2x y − 3 = 0 5xWatch Video in App This browser does not support the video element 348 k 17 k AnswerApply the product rule to 3 x 2 3 x 2 Raise 3 3 to the power of 3 3 Multiply the exponents in (x2)3 ( x 2) 3 Tap for more steps Apply the power rule and multiply exponents, ( a m) n = a m n ( a m) n = a m n Multiply 2 2 by 3 3 Multiply the exponents in (y3)3 ( y 3) 3




If X Y 3 X Y 3 6y X 2 Y 2 K Y 2 Then K A 1 B 2 C 4 D 8 Youtube



2
Solution satisfies φ(x,y) = x2y2 2xy = C 3 (Sec 26 Problem 16) Determine the value of b such that the following equation is exact, and then solve the equation (ye2xyx)dxbxe2xydy = 0 Solution Let M(x,y) = ye2xy x and N(x,y) = bxe2xy We have M y = e2xy 2xye 2xyand N x = be 2bxye2xy So M y = N x if b = 1 Thus there is a functionLeast common multiple of 3 and 5 is 15 Multiply \frac {2xy} {3} times \frac {5} {5} Multiply \frac {3x2y} {5} times \frac {3} {3} To add or subtract expressions, expand them to make their denominators the same Least common multiple of 3 and 5 is 1 5 Multiply 3 2 x y times 5 5 Multiply 5 3 x − 2 y times 3 3 Since \frac {5\left (2xY'\frac{4}{x}y=x^3y^2, y(2)=1 y''ky=0 en Related Symbolab blog posts Advanced Math Solutions – Ordinary Differential Equations Calculator, Exact Differential Equations In the previous posts, we have covered three types of ordinary differential equations, (ODE) We have now reached



2
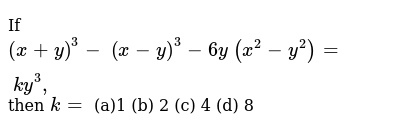



If X Y 3 X Y 3 6y X 2 Y 2 K Y 3 Then K A 1 B 2 C 4 D 8
X^3 x^2 y x y^2 y^3 Natural Language; Perform the indicated operations 1 9 (2) 2 18 ÷ 3 2 Evaluate 3 6x – 3y^2 4 when x = 3 and y = 2 Combine 4 3xy^2 – xy^2 3x^2y Solve for x 5 3x 7 = 2x 5 6 3(x 2) = 27 Solve a read moreGet an answer for '2x 3y = 2 x 3y = 7 find x and y' and find homework help for other Math questions at eNotes



2




Solve The Following Equation 6y 2y 4 A Y 3 B Y 1
Y = c 1 cos t − c 2 sin t, y y = −c 1 sin t − c 2 cos t (c 1 sinIf xy^3xy^36yx^2y^2=ky^2 find k x y³ x y³ If (xy)^3(xy)^36y(x^2y^2)=ky^2, find k Please scroll down to see the correct answer and solution guideClick here👆to get an answer to your question ️ If (x y)^3 (x y)^3 6y(x^2 y^2) = ky^2 , then k =



Systems Of Linear Equations
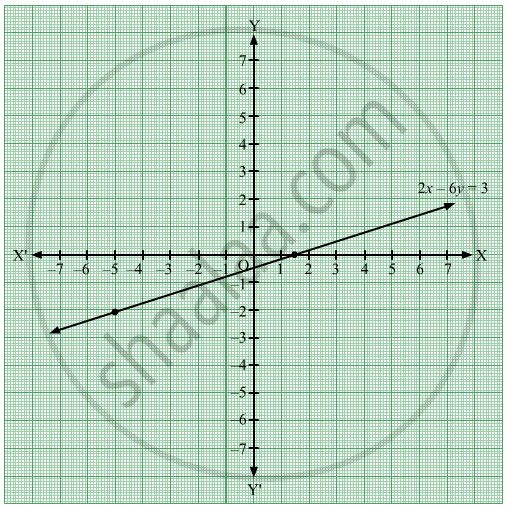



Complete The Following Table To Draw The Graph Of 2x 6y 3 Algebra Shaalaa Com
Es la porción del rectángulo en la que f no se anula La función f es continua en A, portantof esintegrableenA Luego,aplicandoelteoremadeFubini Z A f = Z 2 1 µZ 4 1 f(x;y)dy ¶ dx = Z 2 1 µZ 2x x 1 (xy)2 dy ¶ dx = = Z 2 1 • ¡ 1 xy ‚2x x dx = Z 2 1 You have an Implicit Function in which y is function of x so you have to derive it as well You get (1 ⋅ y2 2xy dy dx) − (3x2y x3 dy dx) = 0 using the Product Rule Then y2 2xy dy dx − 3x2y −x3 dy dx = 0 Collecting dy dx dy dx 2xy − x3 = 3x2y −y2 dy dx = y(3x2 − y) x(2y − x2) Hope it helps(2 x) dy dx = 3y This is a First Order separable Differential equation, and we can rearrange as follows 1 y dy dx = 3 x 2 And we can "separate the variables" to get ∫ 1 y dy = ∫ 3 x 2 dx
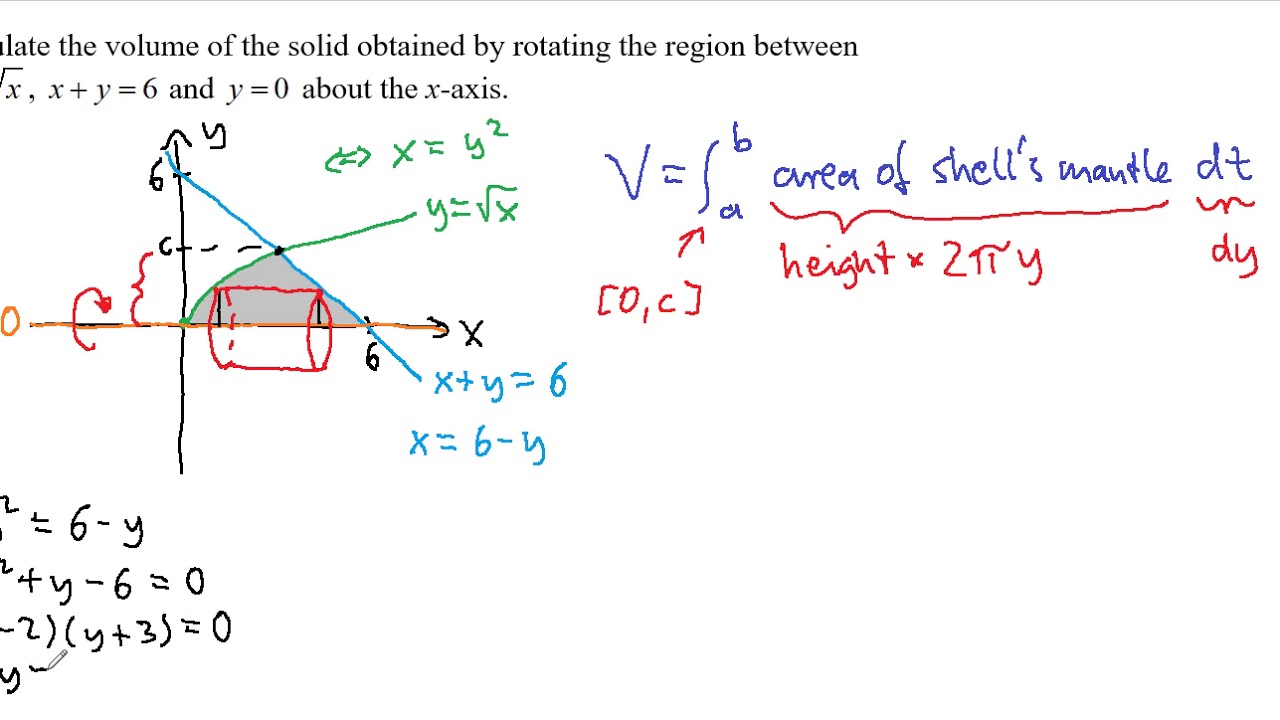



Volume Of Revolution Shell Method



2
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreLet y=0 and solve for x, this is your xintercept 3x3 (0)=6 3x=6 3x/3=6/3 x=2 Plot (2,0) Notice that is the same xintercept that L1 had L1 is lying right ontop of L2, in other words they graphically are the same line The solution is all real numbersThe calculator will try to find the solution of the given ODE firstorder, secondorder, nthorder, separable, linear, exact, Bernoulli, homogeneous, or inhomogeneous Initial conditions are also supported Your input solve $$$ y ' \left (x \right) = x^ {2} $$$




Mai If The Equation Of The Curve On Reflection Of The Ellipse About The Line X
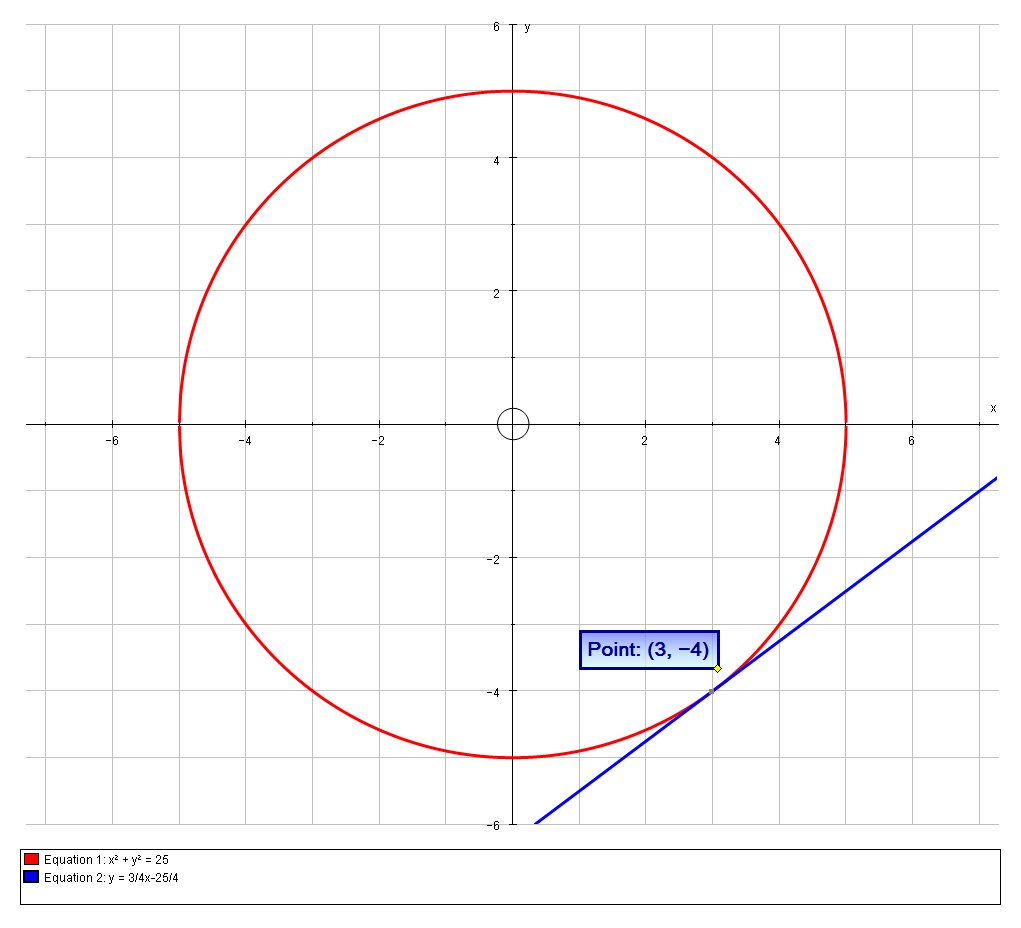



How Do You Find An Equation For The Line Tangent To The Circle X 2 Y 2 25 At The Point 3 4 Socratic
Answer (1 of 2) 3/x2/y=0 take lcm or multiply both lhs and rhs with xy 3y2x=0 3y=2x substitute 3y=2x in the other equation 2/x2/(2x)=1/6 2/x1/x=1/6 as they are like fractions we can perform subtraction 1/x=1/6 therefore x=6 and substituting x=6 in any eqn find the value of yAny tangent to y2 = 4x is y = mx 1m It touches the circle, if 3 = 3m 1m1 m2⇒ 91 m2 = 3m 1m2⇒ 91 m2m2 = 3m2 12⇒ 9m2 9m4 = 9m4 1 6m2⇒ 3m2 = 1⇒ m = ± 13For the common tangent to the above xaxis we takem = 13∴ Equation of common tangent is, y = x3 3⇒ 3y = x 3 Find an answer to your question (x y)^3 (x y)^3 6y(x^2 y^2) = ky^2 find the value of k plz fast rahul3 rahul3 Math Secondary School answered • expert verified (x y)^3 (x y)^3 6y(x^2 y^2) = ky^2 find the value of k



2




If X Y 3 X Y 3 6y X 2 Y 2 K Y 2 Then K A 1 B 2 C 4 D 8 Youtube
If the system of equations 2x 3y – z = 0, x ky 2z = 0 and 2x – y z = 0 has a nontrivial solution (x, y, z), then \(\frac{x}{y} \frac{y}{z} \frac{z}4x 9y 3 (xy) First, we will start by opening the bracket, so the expression becomes; Show activity on this post Your method can't find two other critical points You successfully found that x y = ± 6 and x − y = ± 2, but plus and minus signs don't need to coincide Then four possibilities occur x = 6 2 2 x = 6 − 2 2 x = − 6 2 2 x = − 6 − 2 2 Here 2 and 3 are missing in your attempt




If X Y 3 X Y 3 6y X 2 Y 2 K Y 3 Then K A 1 B 2 C 4 D 8
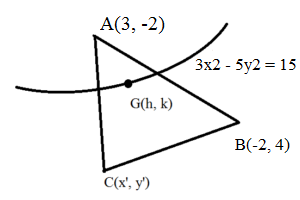



Mathematics Archives Page 2 Of 2 The Fact Factor
Find and sketch the domain of the function of f(x;y) = p x2 y2 The inside of a square root must be nonnegative So f(x;y) is defined only if x2 y2 0 In other words, the domain is x2 y2 0 Note that x2 y2 = (x y)(x y) = 0 Therefore the boundary is the union of two diagonal lines passing through the originLet (h, k) be midpoint of chordThen, its equation is T = S1∴ 3hx 2ky 2x h 3y k = 3h2 2k2 4h 6k⇒ x3h 2 y 2k 3 = 3h2 2k2 2h 3kSince, this line is parallel to y = 2x∴ 3h 22k 3 = 2⇒ 3h 2 = 4k 6⇒ 3h 4k = 4Thus, locus of point is, 3x 4y = 4X y m n 306 19 35 1 300 13 37 13 297 80 19 8 290 171 39 19 286 279 35 9 285 92 17 2 275 42 18 7 273 232 17 4 270 119 37 17 261 2 19 10 260 1 33 7 255 38 16 1 253 12 17 6 247 150 16 3 240 17 31 1 234 115 31 5 230 39 33 13 225 112 17 8 221 84 15 2 216 9 35 19 210 11 31 11 8 57 29 3 7 70 16 7 0 153 33 17 198 175 29 7 195



2
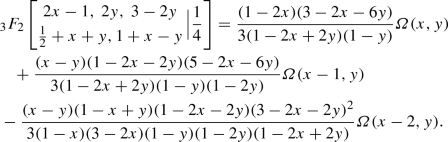



Evaluation Of Nonterminating 3f 2 Frac 1 4 3 F 2 1 4 Series Perturbed By Three Integer Parameters Springerlink




Prove That X Y 3 X Y 3 6y X 2 Y 2 8y 3 Mathematics Topperlearning Com Jd2kccrr
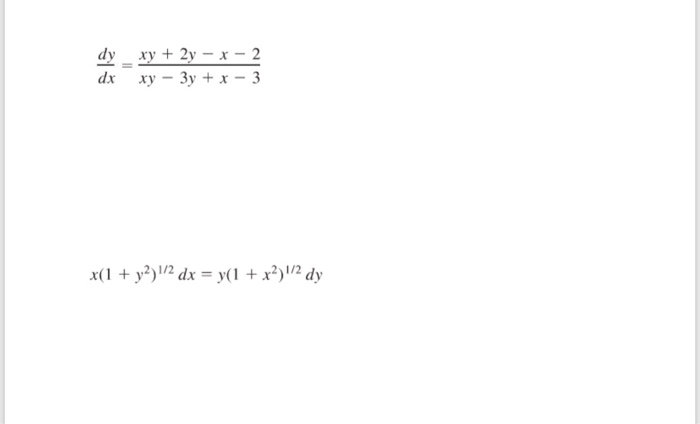



Solved Xy 2y X 2 Xy 3y X 3 Dy Dx Chegg Com




Prove That X Y 3 X Y 3 6y X 2 Y 2 8y 3 Brainly In
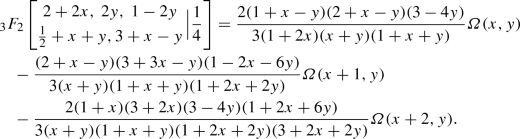



Evaluation Of Nonterminating 3f 2 Frac 1 4 3 F 2 1 4 Series Perturbed By Three Integer Parameters Springerlink




Example If Lines 2x Y 3 0 5x Ky 3 0 Concurrent




2 3 Tangent Plane To A Surface Mathematics Libretexts
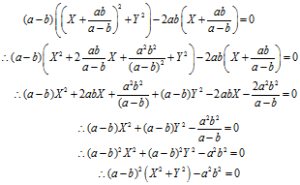



Mathematics Archives Page 2 Of 2 The Fact Factor



2



How To Solve This Find The Equation To The Circle Concentric With The X 2 Y 2 4x 6y 3 0 And Which Touches The Y Axis Quora




Engineering Mathematics Notes



Simultaneous Equations Gmat Math Study Guide
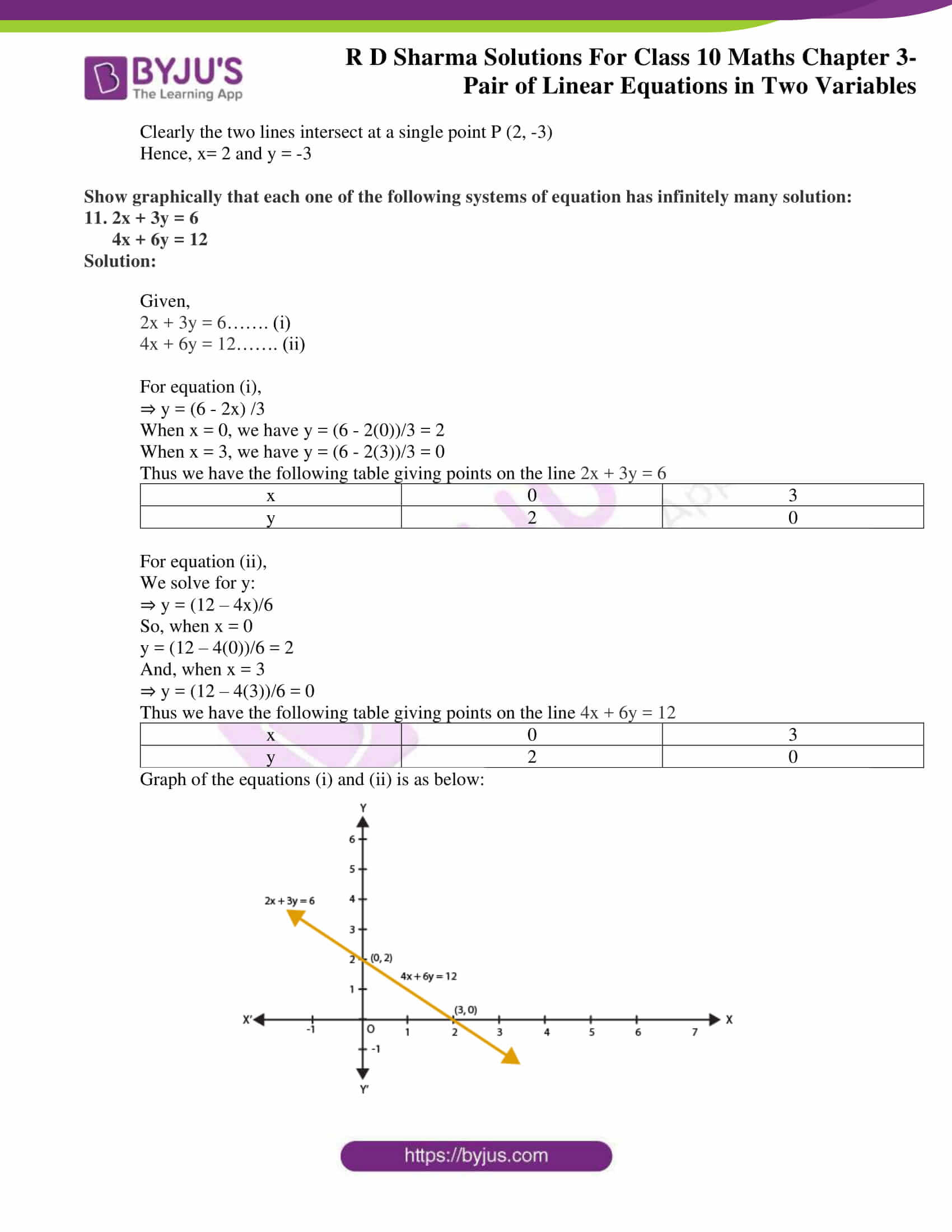



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2



Houstonlibrary Org




Simplify X Y 3 X Y 3 6y X 2 Y 2 Youtube



2




Equation Xy Yx Wikipedia



Evaluation Of Nonterminating 3f 2 Frac 1 4 3 F 2 1 4 Series Perturbed By Three Integer Parameters Springerlink



Parametric Equations For The Intersection Of Planes Krista King Math Online Math Tutor




bestpictjg2x 最高のコレクション Simplify X Y 3 X Y 3 6y X Y X Y




bestpictjg2x 最高のコレクション Simplify X Y 3 X Y 3 6y X Y X Y



Tvwv76qi76mcmm



Nrc Gov




Example If Lines 2x Y 3 0 5x Ky 3 0 Concurrent




3 Find The Solution To Y 6y 8y 16 X 0 0 X 0 0 Given That Y X Ce Cze Homeworklib




bestpictjg2x 最高のコレクション Simplify X Y 3 X Y 3 6y X Y X Y




Simplify X Y 3 X Y 3 6y X 2 Y 2 Youtube



Solved In Exercises 22 27 Solve The Initial Value Problem Chegg Com



2



If X Y 3 X Y 3 6y X 2 Y 2 Ky 2 Then K A 1 Sarthaks Econnect Largest Online Education Community




Linear System Can Be Solve By Graphing It Intersect At X Axis Once




Solved Fid Gcneral Solutions Of The Differential Equations In Prob Lens Through 30 Prinies Denote Derivatives Mith Ruprct 0 X Thrughou 1 Wy 2 Zxyy 2y J Vv Y Y 5 6 Wy Yu Y




If Xy 0 And X 2y 2 Xy 6 Which Of The Following Could Be Y In Te Problem Solving Ps



Solved Given Xy 4 X 2y X 3y Find Y Y Y 4 2 Chegg Com



2



If X Y X Y 6y X Y Ky What Is K Quora



1



1




How Do You Find The Equations Of The Tangent Lines To The Curve Y X 1 X 1 That Are Parallel To The Line X 2y 2 Socratic




Transform X 3 Y 3 3xy 0 Mathematics Stack Exchange




For What Value Of K The Pair Of Linear Equations 3x Y 3 And 6x Ky 8



15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts
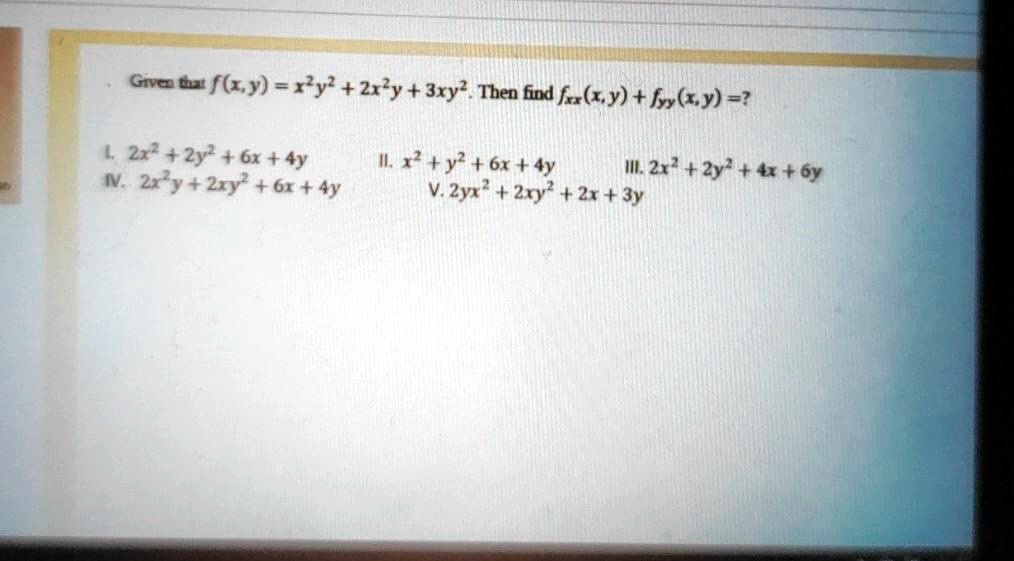



Solved Getf Sy Ry 2rytbry Tben Fnd F Ry H Ky 2r2 2y2 6x 4y X Y2 6x 4y M I 2x 2y 6y 2r7y 2ry2 6r 4y



The Factors Of X 3 X 2 Y Xy 2 Y 3 Are A X Y X 2 Xy Y 2 Sarthaks Econnect Largest Online Education Community




Implicit Differentiation Advanced Example Video Khan Academy



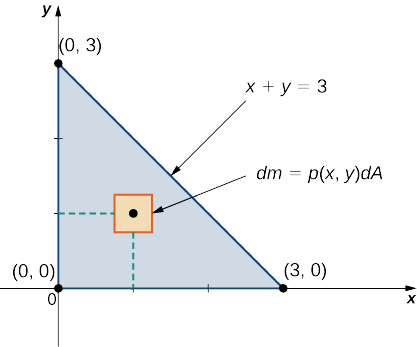
Calculating Centers Of Mass And Moments Of Inertia Calculus Volume 3
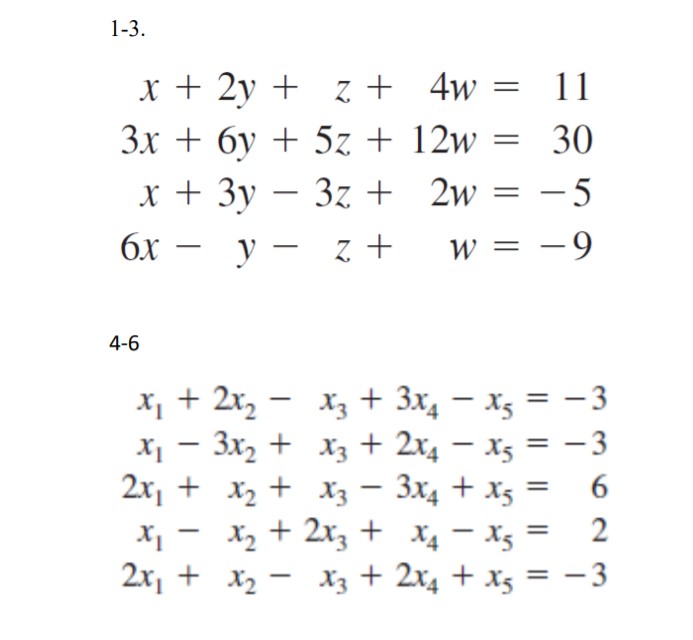



Answered X 2y Z 4w 11 3x 6y 5z 12w Bartleby



2



2




3 Given X Y X Y 6y X2 Y2 Ky Then The Value Of K Is Brainly In




Solved Homework Problems For Handout Sheet 10 1 Solve The De 3x Y Dx Xydy 0 2 Solve The De Y 8x Dx 8xy Dy 0 3 Solve The De 6y Xy Y Dx 2xdy 0 4 Solve The De Xydx X 3 Dy 0 5 Solve The




bestpictjg2x 最高のコレクション Simplify X Y 3 X Y 3 6y X Y X Y



How To Solve For X And Y In X Y 5 And Xy 6 Quora




Which Of The Following Pairs Of Linear Equations Are Consistent Inconsistent If Consistent Obtain The Solution Graphically I X Y 5 2x 2y 10 Ii X Y 8



2



2




If X Y 3 X Y 3 6y X 2 Y 2 K Y 3 Then K A 1 B 2 C 4 D 8



2



2




Simplify X Y X Y 6y X Y Brainly In



How To Solve The Simultaneous Equations X 2 Y 2 36 And X 2y 6 Quora




Solved 1 2 X Y 1 Dx Ydy 0 U Xydx X 2 Y 2 Dy 0 Chegg Com




Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy




Solved Uc Rncr Rules Solve Tha Following System Cuuuona Zx 6y 12 Zy 13 Y 6 2 6 Xy 3 1 Ry 6 2 D Ky 3 1 Cucic Thypethula Identify 44 Write




Maxima And Minima




If 6xy X 2 Y 9y What Is The Value Of Xy Data Sufficiency Ds



X Y 3 X Y 3 Simplify




Solving A System Of Equations Using A Matrix Precalculus Socratic
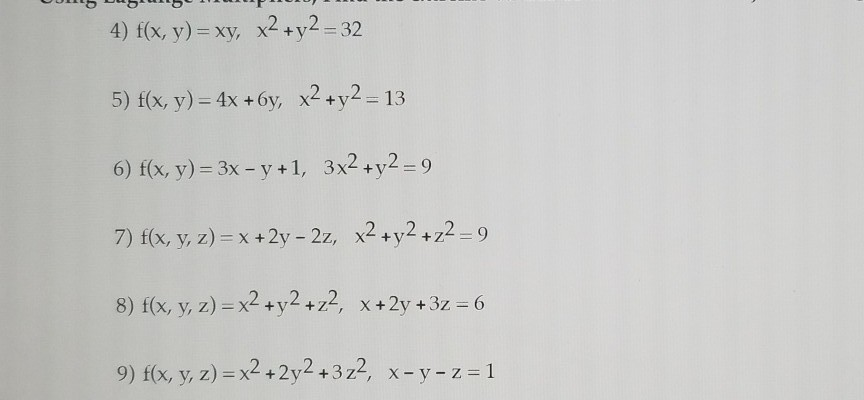



Solved 4 F X Y Xy X2 Y2 3 5 F X Y 4x 6y X2 Y2 Chegg Com



2
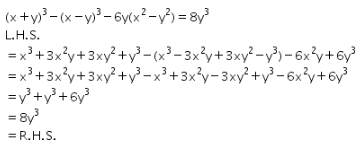



Prove That X Y 3 X Y 3 6y X2 Y2 8y3 Cbse Class 9 Maths Learn Cbse Forum
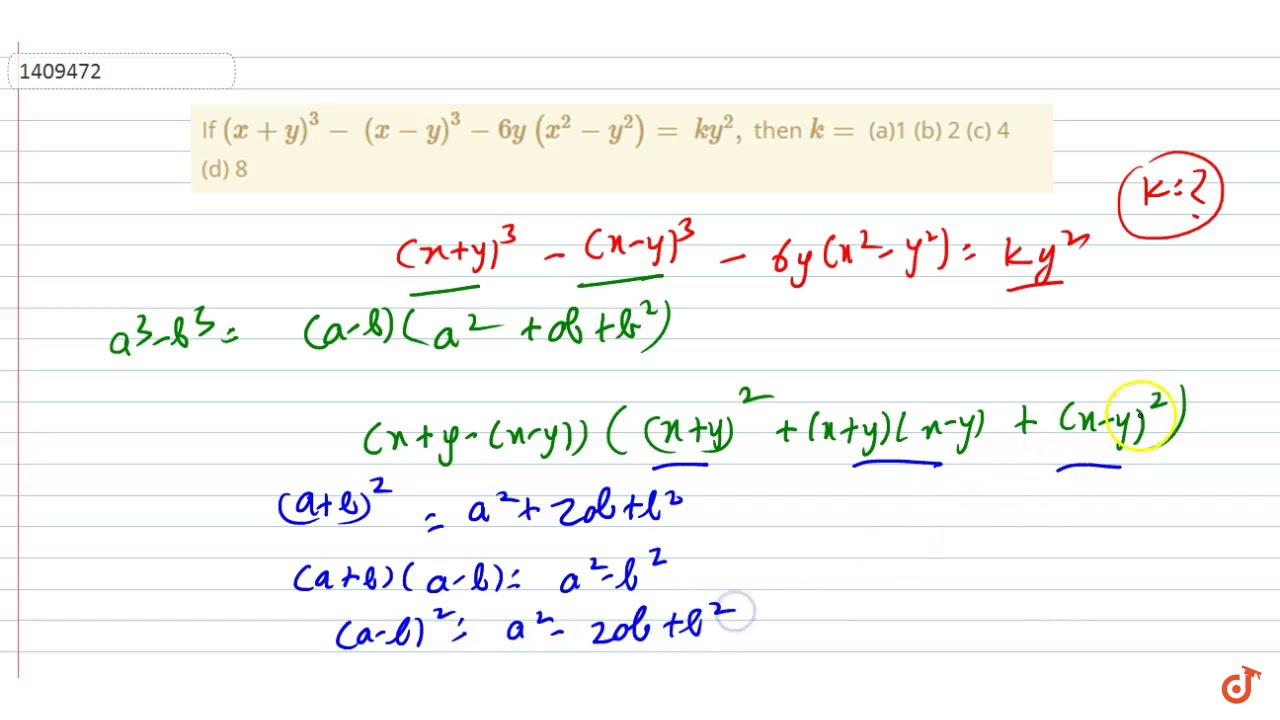



If X Y 3 X Y 3 6y X 2 Y 2 K Y 2 Then K A 1 B 2 C 4 D 8 Youtube




Prove That X Y 3 X Y 3 6y X 2 Y 2 8y 3 Brainly In



Nrc Gov




bestpictjg2x 最高のコレクション Simplify X Y 3 X Y 3 6y X Y X Y



0 件のコメント:
コメントを投稿